优化算法:批量梯度下降、随机梯度下降与小批量梯度下降
Iteration与Epoch
- Iteration: 参数的一次更新,就是一次Iteration
- Epoch:将所有的mini-batch全部计算一遍,称为一次Epoch
批量梯度下降(BGD,Batch Gradient Descent)
批量梯度下降是最基本的优化算法。它在每一次迭代中都使用全部的样本来进行梯度更新。
\[\begin{align} &J(\theta_0,\theta_1,...,\theta_n)=\frac{1}{m}\sum_{i=1}^mcost(i)\\ &for\ j=1,2,...,n \lbrace \\ & \qquad \theta_j := \theta_j-\alpha \frac{\partial J(\theta_0,\theta_1,...,\theta_n)}{\partial \theta_j} \\ & \rbrace \end{align}\]然而,当样本的数目很大时,每次迭代都要对所有的样本进行计算,训练过程会很慢。
随机梯度下降(SGD, Stochastic Gradient Descent)
随机梯度下降在每一次迭代中都仅仅使用一个样本而非全部样本来进行梯度更新,这样每一轮参数的更新速度就快了很多。
\[\begin{align} &J_t(\theta_0,\theta_1,...,\theta_n)=cost(t)\\ &for\ t=1,2,...m \lbrace\\ &\qquad for\ j=1,2,...,n \lbrace \\ & \qquad\qquad \theta_j := \theta_j-\alpha \frac{\partial J_t(\theta_0,\theta_1,...,\theta_n)}{\partial \theta_j} \\ & \qquad\rbrace\\ & \rbrace \end{align}\]随机梯度下降也有一些缺点:
- 准确度下降。即使目标函数时强凸函数,SGD也无法做到线性收敛。
- 陷入局部最优。单个样本不能代表全部样本。
- 不易于并行计算。不能很好的利用计算资源。
小批量梯度下降(MBGD, Mini-Batch Gradient Descent)
小批量梯度下降是介于梯度下降和随机梯度下降之间的一个算法。它将样本平均分为多个部分,在每一次迭代中只采用一个部分来对参数进行更新。它比前两个算法要多一个超参数batchSize,代表着每一部分的大小,
\[\begin{align} &J_t(\theta_0,\theta_1,...,\theta_n)=\sum_{i=(t-1)*batchSize}^{t*batchSize-1}cost(i)\\ &for\ t=1,2,...m/batchSize \lbrace\\ &\qquad for\ j=1,2,...,n \lbrace \\ & \qquad\qquad \theta_j := \theta_j-\alpha \frac{\partial J_t(\theta_0,\theta_1,...,\theta_n)}{\partial \theta_j} \\ & \qquad\rbrace\\ & \rbrace \end{align}\]可见,当batchSize=m的时候,MBGD就变成了BGD,当batchSize=1时MBGD就变成了SBGD。它既减少了每次迭代的计算量和收敛所需要的迭代次数,又可以使最终结果更加接近梯度下降的结果。并且可以充分利用部件进行并行化运算。
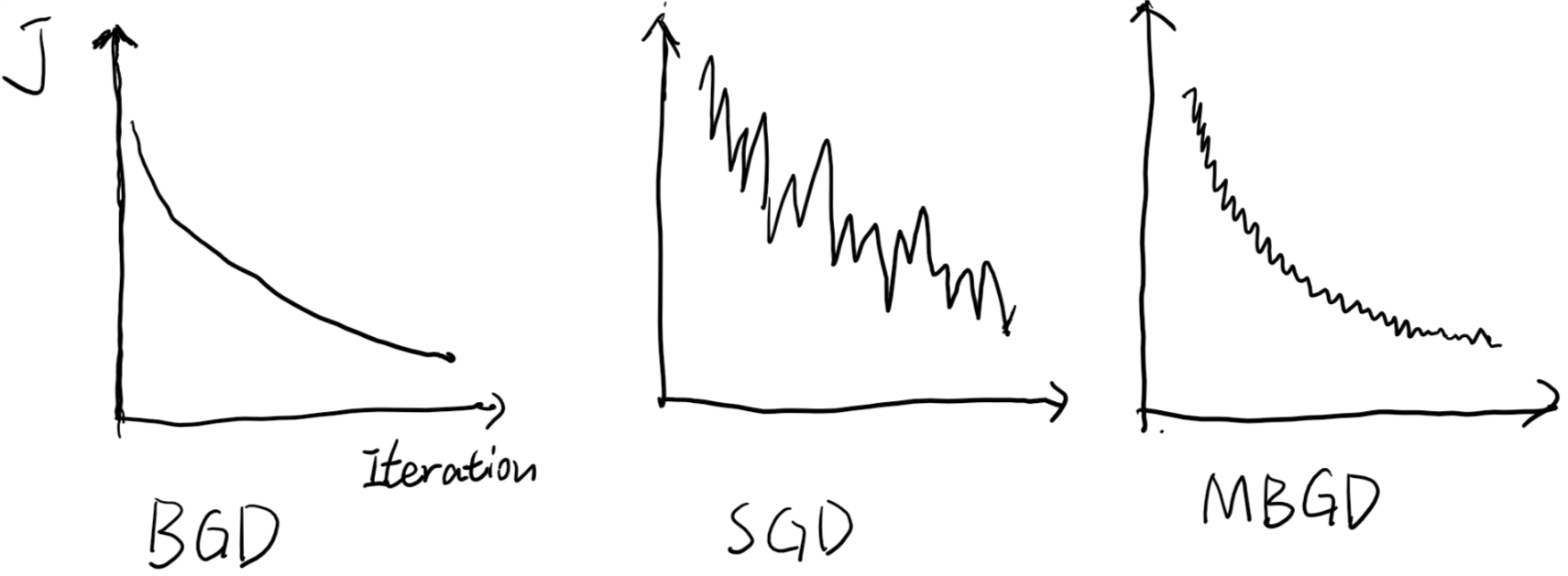

显然,batchSize的选取直接影响到优化算法的效率。在选择batchSize的时候,我们要注意:
- 如果训练集比较小(m<=2000),使用BGD。
- 训练集比较大时,常选用的batchSize有:64、128、256、512。计算机内存的布局和访问方式决定了当你的batchSize的大小是2的指数倍时,你的代码会运行的更快。
课程链接: