加速神经网络的训练过程
归一化(normalization)
归一化使得损失函数更易于优化,在更少的迭代次数内就可以达到同样的优化效果,它的步骤如下:
- 求均值: \(\mu = \frac{1}{m} \sum_{i=1}^m x^{(i)}\)
- 求方差: \(\sigma^2 = \frac{1}{m} \sum_{i=1}^m (x^{(i)})^2\)
- 减去均值再除以方差: \(x := \frac{x-\mu}{\sigma^2}\)
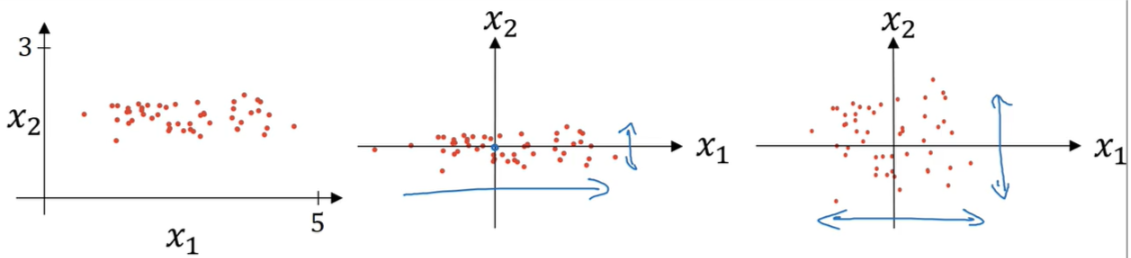
原训练集、减去均值、减去均值并除以方差的三个图像如下:
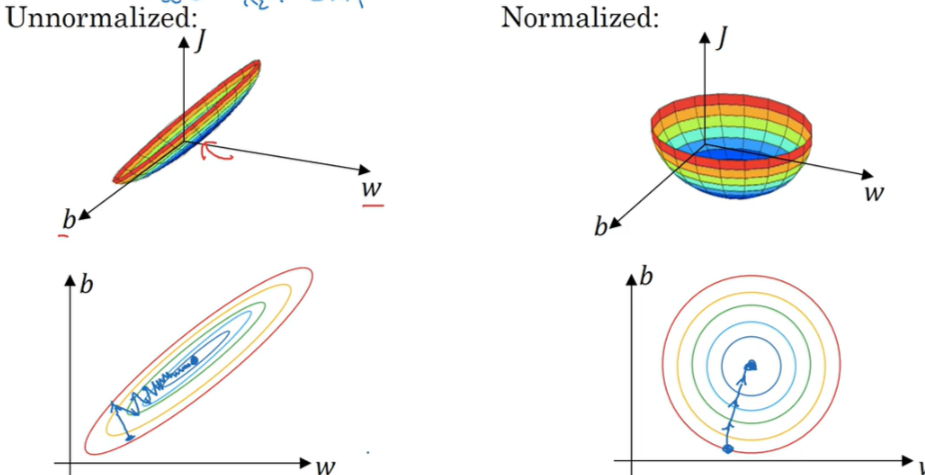
正则化后与没有正则化的损失函数对比:
梯度消失/梯度爆炸(vanishing/exploding gradients)
在训练神经网络,尤其是层数非常多的神经网络的时候,我们会遇到一个问题,就是梯度的消失和爆炸。
梯度消失问题发生时,离输出层最近的隐藏层相对正常,但从后往前隐藏层的权重更新的会越来越慢,甚至导致前面的层权值几乎一直保持一开始的权重不变,这就导致前面的隐藏层相当于只是一个映射层,对所有的输入做了一个同一映射,这是此深层网络的学习就等价于只有后几层的浅层网络的学习了。
而梯度爆炸则与梯度消失相反。此时前面的层会比后面的层更新的要快很多,前面的参数可能会无限大或是无限小,模型也就废了。
其实梯度爆炸和梯度消失问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题,可以考虑用ReLU激活函数取代sigmoid激活函数。另外,LSTM的结构设计也可以改善RNN中的梯度消失问题。
权重初始化
更仔细地设置初始权重会有助于削弱梯度消失和梯度爆炸。
对于一个神经元,我们知道:
\[z^{(l+1)} = W^{(l)}a^{(l)}\]我们希望上层神经元的数目n越多,权重矩阵的每个值就越小。一个合理的做法就是设置权重的方差等于n的倒数。
\[Var(w_i) = \frac{1}{n}\]# 适用于relu函数
W[l] = np.random.randn(shape) * np.sqrt(2/n[l-1])
# 适用于leak-relu函数
W[l] = np.random.randn(shape) * np.sqrt( 2/((1+alpha**2)*n[l-1]) )
# Xavier初始化,适用于tanh函数
W[l] = np.random.randn(shape) * np.sqrt(1/n[l-1])
# 适用于tanh函数
W[l] = np.random.randn(shape) * np.sqrt(1/(n[l-1]+n[l]))
课程链接: