激活函数比较
在建立神经网络的时候，你需要为隐含层和输出层选择激活函数。若不选择任何激活函数，那么我们称之为感知机，它和没有任何隐藏层的线性回归没有任何区别（多个线性函数的组合仍然是线性函数）；若只在输出层设置激活函数为sigmoid函数，那它其实和没有任何隐藏层的逻辑回归模型也是一样的。一般来说唯一可以使用线性激活函数的地方只有输出层，此外只有在一些极为特殊的情况下才会使用，比如压缩有关的处理。所以我们需要找一些非线性函数作为激活函数。
sigmoid
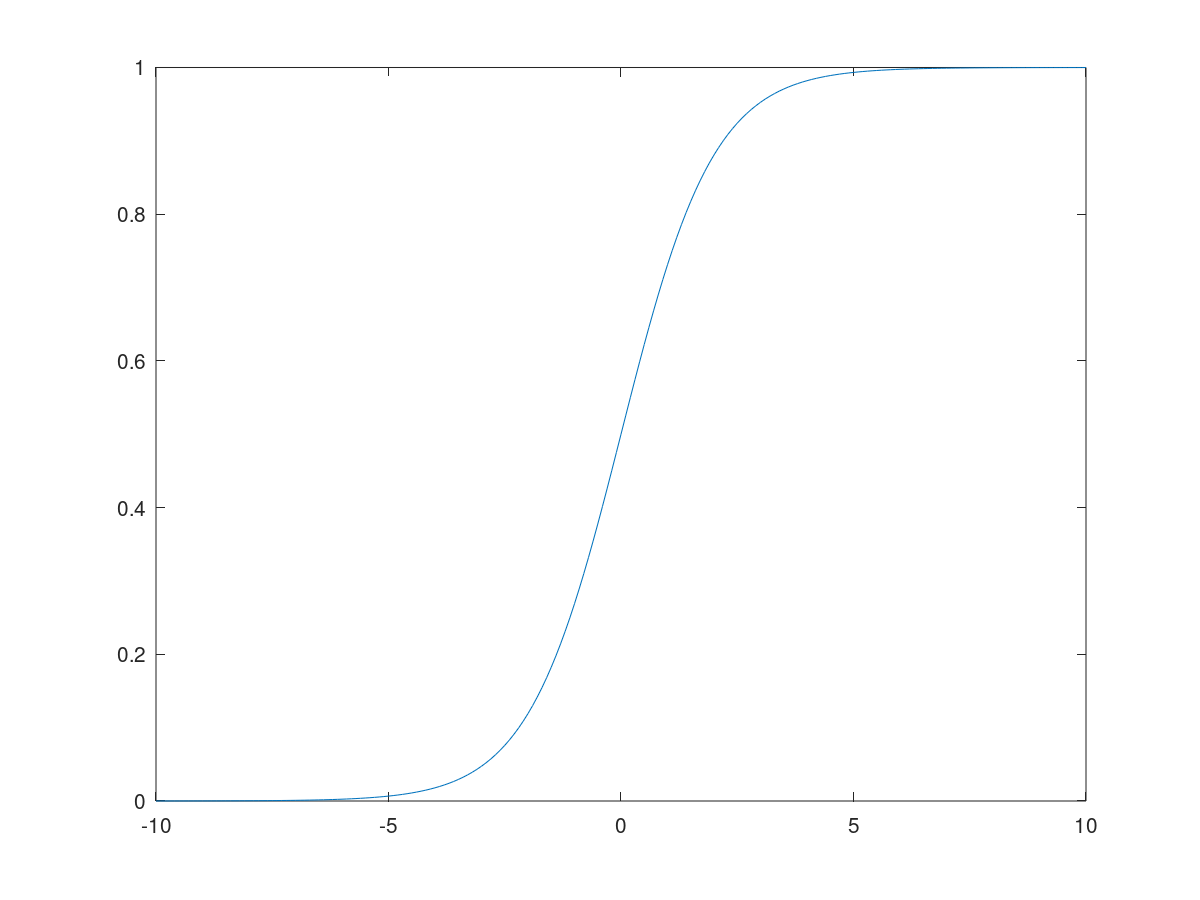
sigmoid函数就是我们在逻辑回归中所使用的函数。它可以将变量映射到0~1的范围内，得到类似于概率的输出。他的应用一般仅限于二分类问题的输出层。
函数方程：
\[sigmoid(z) = \frac{1}{1+e^{-z}}\]导数：
\[\frac{d}{dz} sigmoid(z)=sigmoid(z)*(1-sigmoid(z))\]函数图像：
tanh
tanh函数即双曲正切函数，从数学的角度看可以认为它是sigmoid函数向下拉伸的结果。一般来说采用tanh函数会比采用sigmoid函数作为激活函数的效果要好。它将变量映射到-1到1的范围内，因此隐藏层激活函数输出的平均值一般会更加趋向于0，达到数据中心化的效果。而数据中心化可以使得下一层的学习变得更简单一点。但是有一个特例，当你对数据进行二分类的时候，可以在输出层使用sigmoid激活函数。
函数方程：
\[tanh(z) = \frac{e^z - e^{-z}}{e^z+e^{-z}}\]导数：
\[\frac{d}{dz}tanh(z) = 1-(tanh(z))^2\]函数图像：
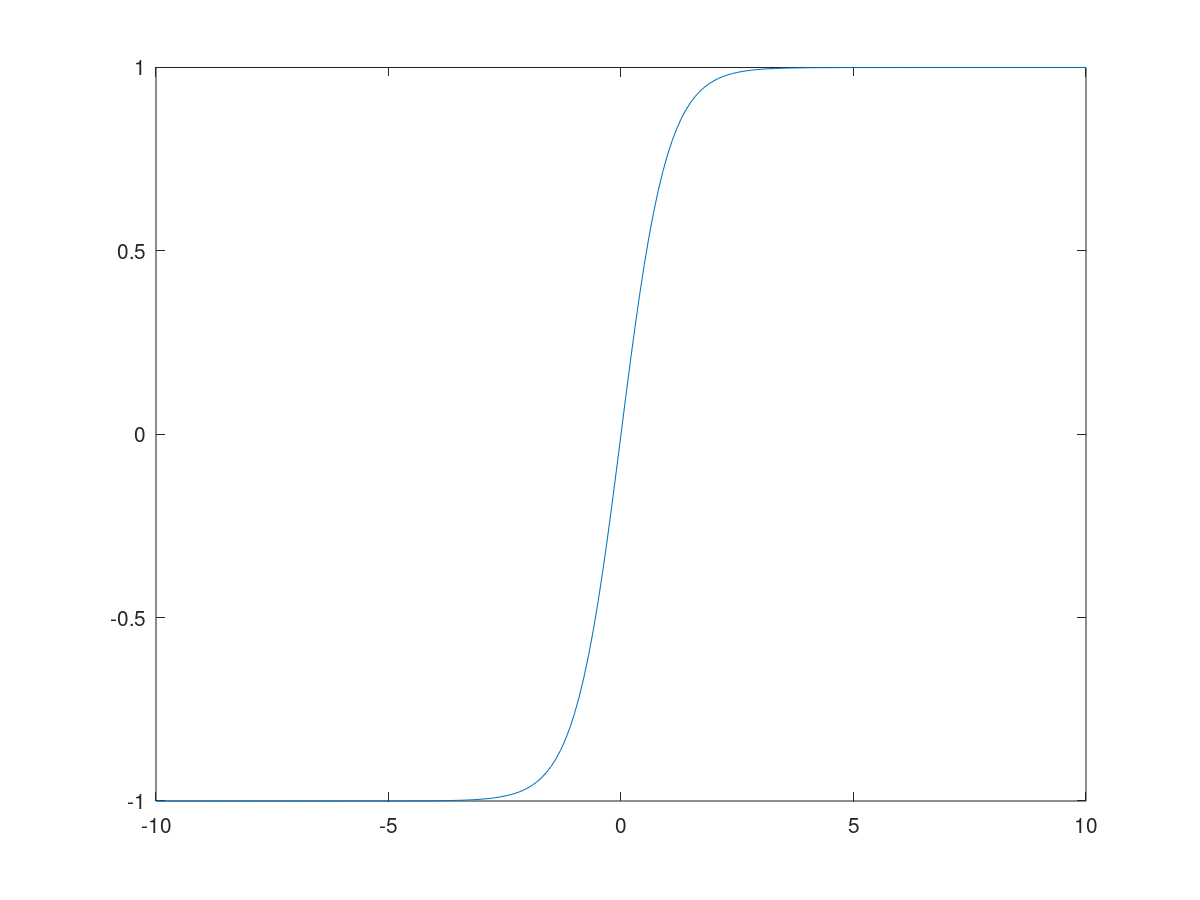
然而，从它们的图像中我们可以看出，不论是sigmoid函数还是tanh函数都有一个缺点：当z很大或很小时，他们的梯度就会变得非常小，甚至接近于0，收敛的会很慢。而relu函数则很好的解决了这个问题，并成为现在人们最常用的激活函数。
ReLU
ReLU是 rectified linear unit 的简称，即线性整流函数。它在原点左侧的梯度都为0，在原点右侧的梯度都为1.这样它收敛的就会比较快。从数学上讲，ReLU函数在原点不可求导，我们可以人为地设置0点的导数为0或是1。同样的，当处理二分类问题时，我们可以设置隐含层为ReLU函数，输出层为sigmoid函数。
函数方程：
\[ReLU(z) = max(0, z)\]导数
\[\frac{d}{dz} relu(z)= \begin{cases} 0 \quad if\ z<0\\ 1 \quad if\ z>0\\ undefined \quad if\ z=0\ (可人为地设为0或1) \end{cases}\]函数图像：
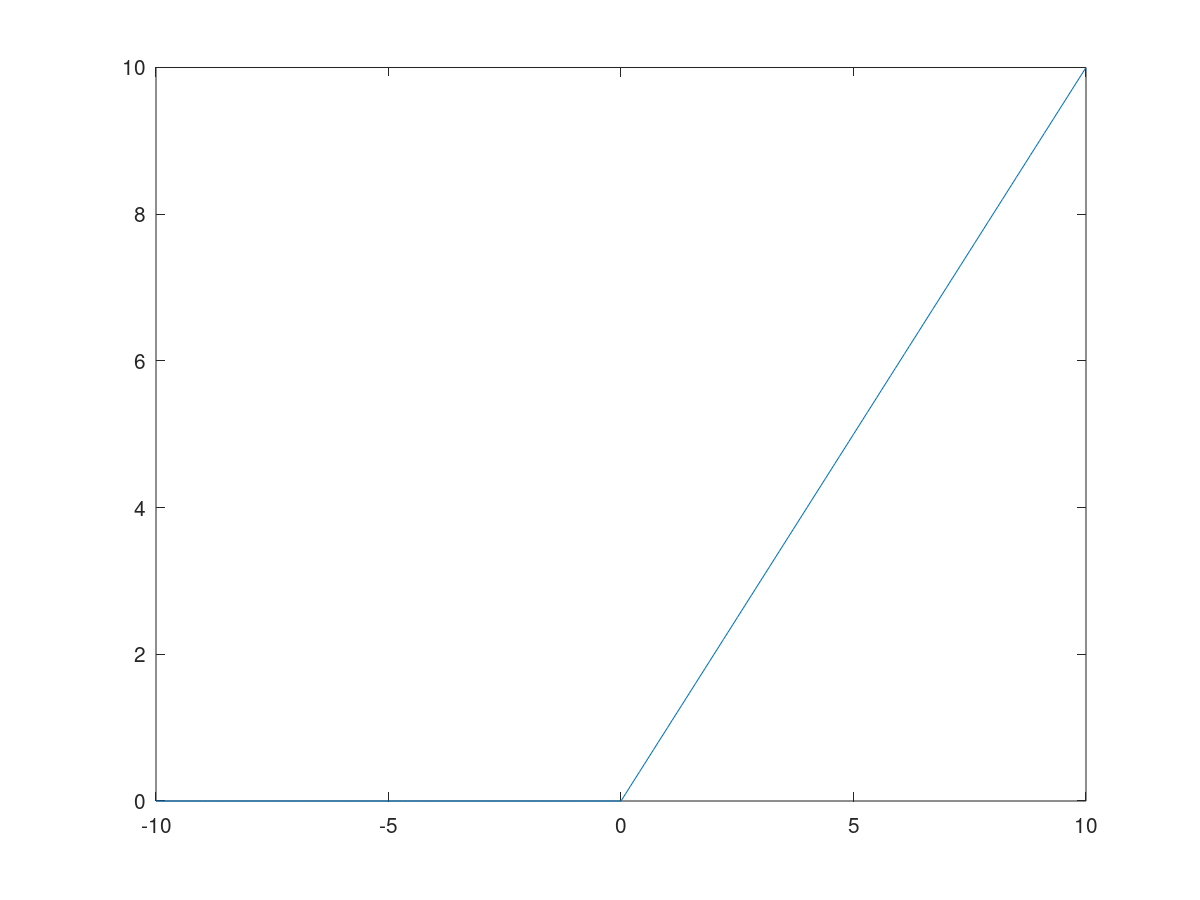
ReLU的一个缺点是当z是负数时，它的导数为0，但在实际应用中你有足够多输出值z大于0的隐含层，学习速率仍然会很快，这并不是问题。
LeakyReLU
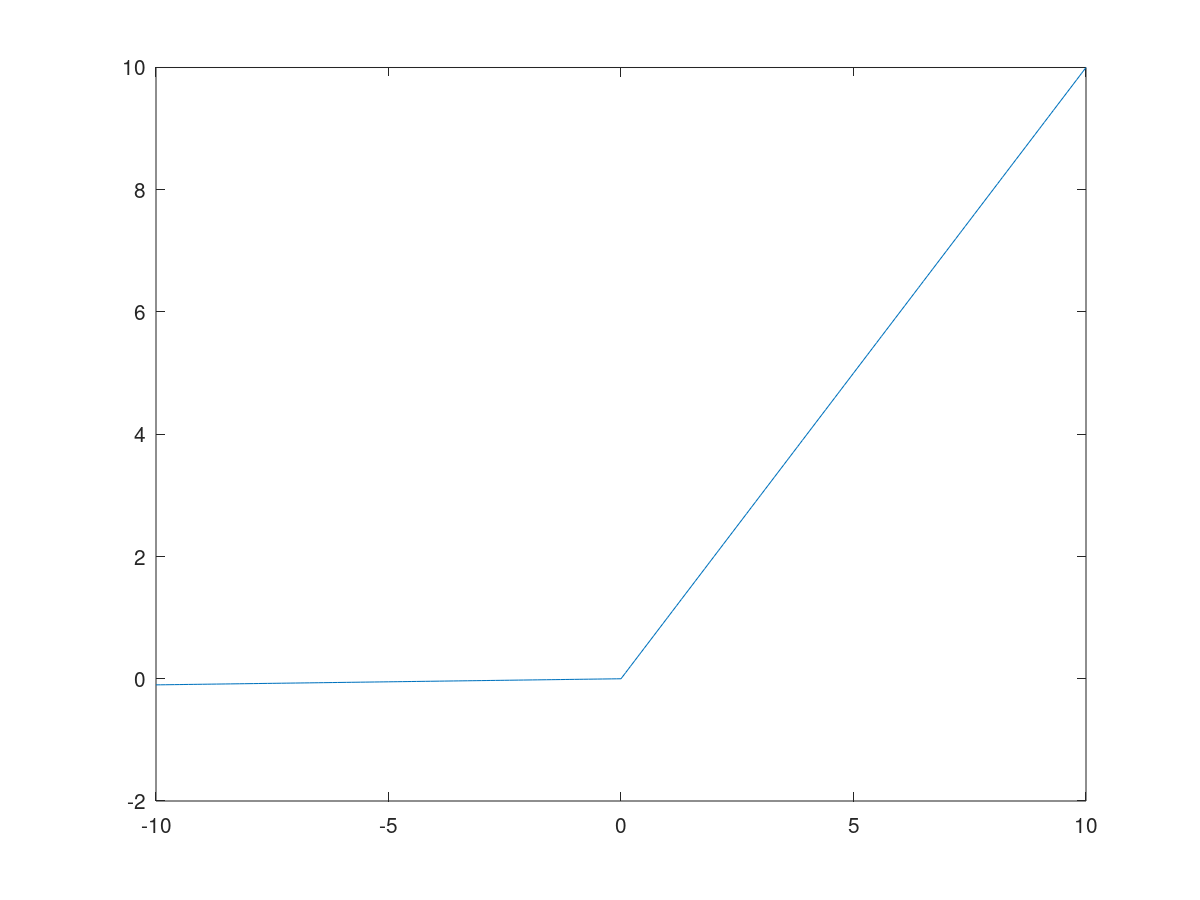
LeakReLU解决了ReLU在z为负数的情况下导数为0的问题。尽管在实际应用中并不常见，但它一般表现得要比ReLU激活函数要好。
函数中的0.01这个常数会使得函数左侧稍微倾斜，我们完全可以把它看作算法的另一个参数，但实际上很少有人会这么做。
函数方程：
\[LeakyReLU(z) = max(0.01z, z)\]导数：
\[\frac{d}{dz} LeakyRelu(z)= \begin{cases} 0.01 \quad if\ z<0\\ 1 \quad if\ z>0\\ undefined \quad if\ z=0\ (可人为地设为0,01或1) \end{cases}\]函数图像：
softmax
softmax是一种用于输出层的函数。之前我们讲过sigmoid一般用于二分类问题的输出层，而与之相对相应softmax用于多分类问题的输出层。与其它所有激活函数不同的是，它的输入和输出都是一个向量。令C为所有类的数量的总和，当C=2且只有输入层和输出层时，softmax就退化为logistic regerssion，此时只需计算其中一类的概率，而1减去第一类的概率即为第二类的概率。
函数方程：
\[t = e^{(z^{[L]})}\\ a^{L} = \frac{t}{\sum_{j=1}^{C}t_j}\\\]导数：
\[\frac{\partial\ a_j}{\partial z_i}= \begin{cases} -a_i a_j \quad i \neq j \\ a_i(1-a_i) \quad i=j \end{cases}\]使用分类交叉熵函数作为代价函数，且最后一层为softMax时，最后一层的偏差为：
\[\frac{\partial J}{\partial z} = \hat{y}-y\]当没有隐藏层，只有一个输入层和一个输出层，且输出层使用softmax函数时，任意两个类之间的分界线是线性的：
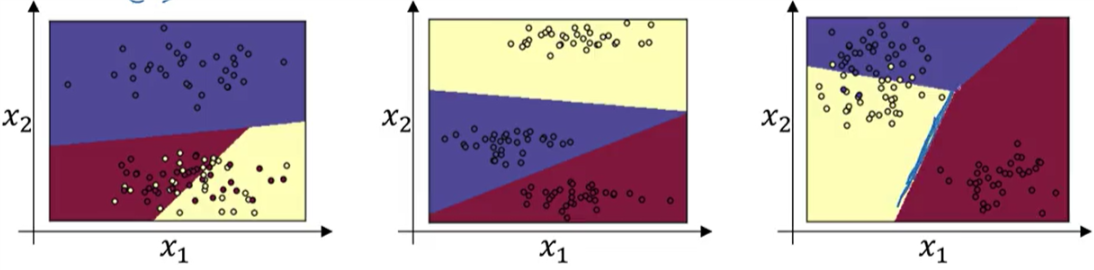
当有隐藏层，且存在隐藏层的激活函数为非线性函数时，任意两个类之间的分界线可能是非线性的。
softmax的输出的向量的每个元素的值在0~1之间，且和为1。与之相对应的是hardmax，hardmax的输出的向量的元素中只有一个为1（概率最大的那一类），其余都为0。
输出层激活函数与代价函数的选取
| 任务类型 | 输出层激活函数 | 代价函数 | 代价函数表达式 |
|---|---|---|---|
| 回归 | Linear | 均方误差(MSE) | \(J(y,\hat{y})= \frac{1}{2m} \sum_{i=1}^m \mid\mid y_i-\hat{y_i} \mid\mid_2^2\) |
| 二分类 | Sigmoid | 二值交叉熵（Binary cross-entropy） | \(\begin{align} J(y,\hat{y}) = &- \frac{1}{m} \sum_{i=1}^m y_i \log \hat{y_i} \\ & - \frac{1}{m} \sum_{i=1}^m(1-y_i)\log(1-\hat{y_i})\end{align}\) |
| 多分类 | SoftMax | 分类交叉熵（Categorical cross-entropy） | \(J(y,\hat{y})=- \frac{1}{m} \sum_{i=1}^m \sum_{j=1}^n y_{(i,j)} \log \hat{y_{(i,j)}}\) |
总结
- 只在二分类问题的输出层使用sigmoid函数作为激活函数。tanh函数严格优于sigmoid函数。
- ReLU函数是最常用的激活函数。当你不知道该用哪个时，就选它。
- 最好是都试一下，选择最合适的。
参考资料：