bp神经网络
代价函数
- 令:
- m = 样本的数量
- n = 参数的数量
- L = 网络的总层数
- \(s_l\) = 第l层单元的数量(不包括偏差单元)
- K = \(s_l\) = 最后一层即输出层的单元个数 = 类的个数 (K>=3)
- \(h_\Theta(x) \in \mathbb{R}^K\) , 且 \({(h_\Theta(x))}_k\) = 第k个输出 = x是第k类的概率
- \(y_k^{(i)}\) = 第i个样本是否为第k类,是为1,不是为0。
- 损失函数:
- 逻辑回归: \(J(\theta) = -\frac{1}{m} [\sum_{i=1}^my^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2\)
- 神经网络: \(J(\Theta) = -\frac{1}{m}[\sum_{i=1}^m \sum_{k=1}^K y_k^{(i)} \log(h_\Theta(x^{(i)}))_k + (1-y_l^{(i)}) \log (1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}}(\Theta_{ji}^{(l)})^2\)
反向传播算法
图示:
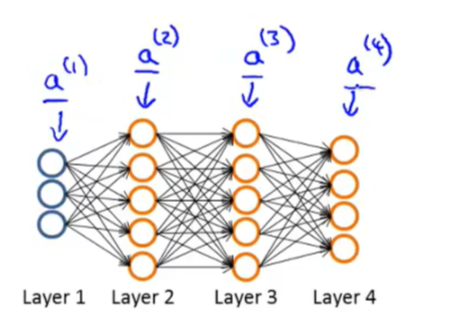
对给定的训练集:\(\{(x^{(1)}, y^{(1)}),...,(x^{(m)}, y^{(m)})\}\)
\(\delta_j^{(l)}\) 表示样本在第l层的第j个神经元的误差。
\(\delta_j^{(l)} = \frac{\partial}{\partial z_j^{(i)}} cost(i)\)
设置 \(\Delta_{i,j}^{(l)}\)
- 设\(a^{(1)}:=x^{(t)}\)
- 执行正向传播(forward propagation)来计算 \(a^{(l)}\) (l=2,3,…L) :
\(a^{(1)} = x\\ z^{(2)} = \Theta^{(1)}a^{(1)}\\ a^{(2)} = g(z^{(2)}) \; (add \; a_0^{(2)})\\ z^{(3)} = \Theta^{(2)}a^{(2)}\\ a^{(3)} = g(z^{(3)}) \; (add \; a_0^{(3)})\\ z^{(3)} = \Theta^{(3)}a^{(3)}\\ a^{(4)} = h_\Theta(x) = g(z^{(4)})\quad (忽略正则项)\\\) - 反向传播部分的第一步是计算 \(\delta^{(L)}=a^{(L)}-y^{(t)}\)
其中L是我们的总层数,\(a^{(L)}\) 是最后一层的激励单元的输出向量。所以我们最后一层的“误差值”就是我们最后一层的输出与正确值的差。
\(\delta_j^{(L)} = a_j^{(L)} - y_j = (h_\theta(x))_j-y_j\\\) - 为了得到最后一层之前所有层的delta值,我们可以使用一个方程来从右到左求解。
\(\delta^{(l)} = \frac{\partial}{\partial z_j^{(l)}} cost(i) = (\Theta^{(l)})^T\delta^{(l+1)}.*g'(z^{(l)}) \quad (l= 2,3,...,L-1)\\ g'(z^{(l)}) = a^{(l)}.*(1-a^{(l)})\\\) - 更新delta矩阵(将所有样本的偏差累加起来):
\(\frac{\partial}{\partial\Theta_{i,j}^{(l)}}cost(i)=a_j^{l}\delta_i^{(l+1)} \\ \Delta_{i,j}^{(l)} := \Delta_{i,j}^{(l)}+a_j^{(l)}\delta_i^{(l+1)}\)
或者向量化:
\(\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T\)
由此我们得到我们新的delta矩阵- \[D_{i,j}^{(l)}:=\frac{1}{m}(\Delta_{i,j}^{(l)}+\lambda\Theta_{i,j}^{(l)}),\ if\ j \ne 0\]
- \(D_{i,j}^{(l)} := \frac{1}{m} \Delta_{i,j}^{(l)},\ if\ j=0\)
这个大写的delta矩阵D作为累加器随着时间的推移来把我们的值加起来,并且最终计算我们的骗到。由此我们得到:
\(\frac{\partial}{\partial\Theta_{i,j}^{(l)}}J(\Theta) = a_j^{(l)}\delta_i^{(l+1)}\)
伪代码
\(Set \ \Delta_{i,j}^{(l)}=0\quad(for\ all\ l,i,j)\\
For\ i=1\ to\ m\\
\qquad Set\ a^{(1)}=x^{(i)}\\
\qquad Perform\ forward\ propagation\ to\ compute\ a^{(l)}\ for\ l=2,3,...,L\\
\qquad Using\ y^{(i)},compute\ \delta^{(L-2)},...,\delta^{(2)}\\
\qquad Compute\ \delta^{(L-1)},\delta^{(L-2)},...,\delta^{(2)}\\
\qquad \Delta_{i,j}^{(l)}:=\Delta_{i,j}^{(l)}+a_j^{(l)}\delta_i^{(l+1)}\\
D_{i,j}^{(l)}:=\frac{1}{m}\Delta_{i,j}^{(l)}+\lambda\Theta_{i,j}^{(l)}\quad if\ j \ne 0 \\
D_{i,j}^{(l)}:=\frac{1}{m}\Delta_{i,j}^{(l)}\quad if\ j = 0 \\\)
其中:
\(\frac{\partial}{\partial\Theta_{i,j}^{(l)}}J(\Theta) = D_{i,j}^{(l)}\)
推导
图示:
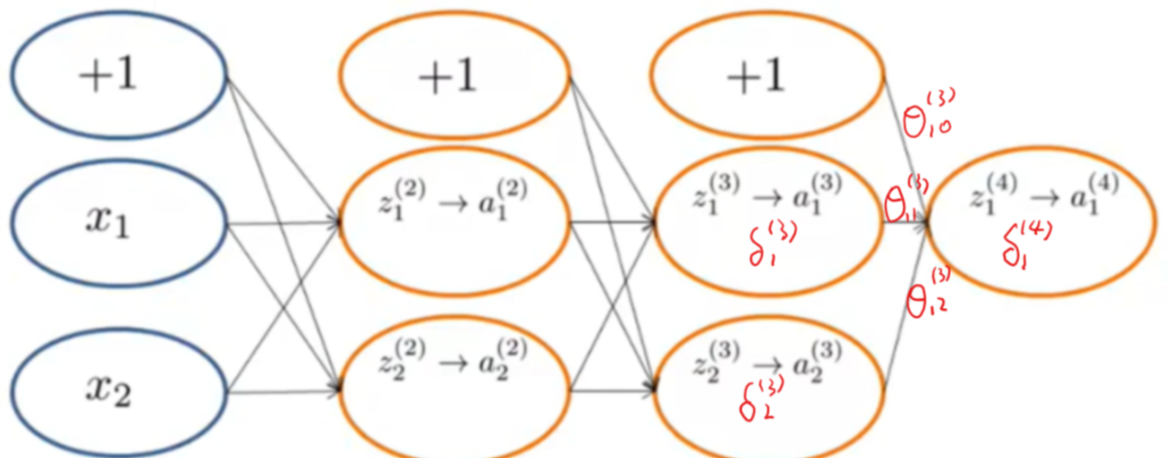
推导过程:

课程链接: