神经网络
为什么需要神经网络?
- 虽然我们已经有了线性回归和逻辑回归,但是当面对很多特征值,决策边界又是非线性的复杂的曲线的问题时,假设函数就会变得十分复杂,需要消耗大量的计算资源。 我们用神经网络来解决复杂的非线性的假设
模型表示
- 神经模型:逻辑单元
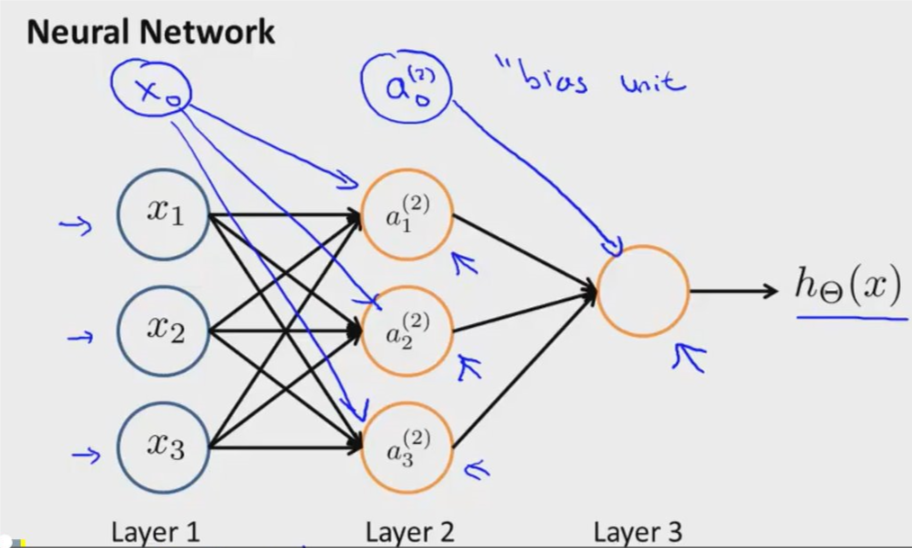
- 其中,layer1又被称为输入层(input layer),最后一层layer被称为输出层(output layer),而他们之间的被称为隐藏层(hidden layer)。
- \(x_0\) 被称为 bias unit,它总是等于1。
- 输入层为输入的不同的特征值,输出层为参数确定后的假设函数。也可以看作是第一层的 activation
- a为 sigmoid function / sigmoid activation function / logistical activation function. \(a_i^{(j)}\) 时第j层的第i个单元的“activation”。
- \(\Theta _{(j)}\) 为映射第j层到第j+1层的权重控制矩阵(weights controlling function)
\(a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \\ a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \\ a_1^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \\ h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + Theta_{11}^{(2)} a_1^{(2)} + \Theta_{12}^{(2)} a_2^{(2)} + \Theta_{13}^{(2)} a_3^{(2)})\)
\(\Theta \in \mathbb{R}^{3 \times 4}\)
即若网络的第j层有\({s_j}\)个单元,第j+1层有\({s_{j+1}}\)个单元,则\(\Theta^{(j)}\)的维度为\(s_{j+1} \times s_j\)
正向传播(forward propagation):实现向量化
- 对之前的公式,令 \(a_i^{(j)} = g(z_i^{(j)})\)
\(x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} \quad z^{(2)} = \begin{bmatrix} z_1^{(2)} \\ z_2^{(2)} \\ z_3^{(2)} \\ \end{bmatrix}\\ z^{(2)} = \Theta^{(1)}x \\ a^{(2)} = g(z^{(2)})\\ 添加 a_0^{(2)} = 1 \\ z^{(3)} = \Theta^{(2)}a^{(2)} \\ h_\Theta(x) = a^{(3)} = g(z^{(3)})\)
神经网络学习它自己的特征
- 神经网络可以由很多层组成,把上一层的输出作为自己这一层的输入的特征
课程链接: