解决过拟合问题
过拟合问题
- 概念
如果我们有过多的特征值,假设函数可能会更加拟合训练集,但是难以泛化到新的例子。 - 高偏差(hign bias) / 欠拟合(underfitting)
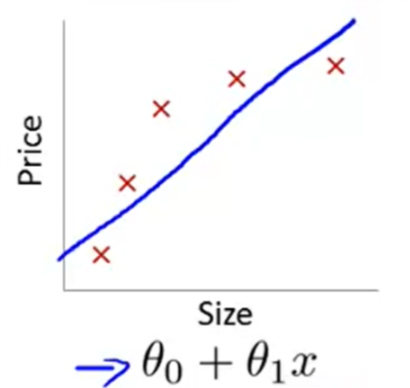
- 拟合(fitting)
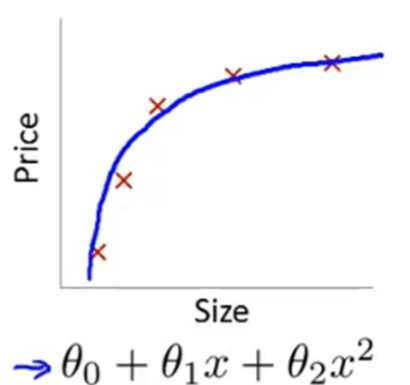
- 过拟合(overfitting)
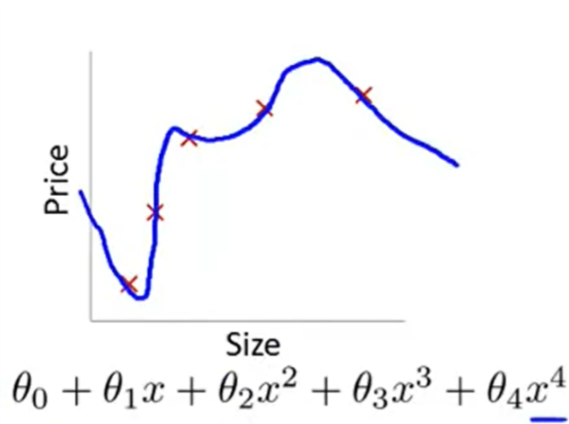
- 如何解决过拟合问题?
- 减少特征值的数量
- 手动选择需要保留的特征。
- 模型选择算法(model selection algorithm)
- 正则化
- 保留全部特征,但是减小参数 \(\theta\) 的值或量级
- 在我们拥有大量的特征值时会很有效,每个参数只会对预测值产生较小的影响。 我们可以通过正则化(regularization)来解决过拟合问题。
- 减少特征值的数量
正则化代价函数
- 正则化 参数取值越小,就对对模型产生更小的影响,产生更简单的假设函数,更不易发生过拟合
- 举例:
假设对房价进行预测,有m+1个样本,n+1个特征以及n+1个参数,由于我们不知道应该缩小哪几个,所以我们要缩小全部的参数。
通过为代价函数添加正则化项来缩小参数。
通常,正则化项只对 \(\theta_1 \sim \theta_{100}\) 进行正则化,因为仅仅去掉一个参数\(\theta_0\)只会产生很小的影响,加不加并没有什么太大的区别,去掉写起来比较方便。- 线性回归:
\(J(\theta) = \frac{1}{2m} [\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2 \quad + \lambda \sum_{j=1}^n \theta_j^2\) - 逻辑回归:
$$ J(\theta) = \frac{1}{m} \sum_{(i=1)}^m[-y^{(i)}log(h_\theta(x^{(i)})) - (1-y^{(i)})log(1-h_\theta(x^{(i)}))]
- \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 $$
- 线性回归:
- 其中, \(\lambda\) 被称为正则化参数(regularization parameter),其作用是控制两个目标间的平衡:假设能很好的适应训练集和保持较小的参数。
- 当正则化参数过大时会导致除第一个参数外的所有参数都趋于0,欠拟合;过小就起不了什么作用。
正则化线性回归
-
梯度下降
\(Repeat\{ \\ \theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)} \\ \theta_j := \theta_j(1-\alpha\frac{\lambda}{m}\theta_j ) - \alpha \frac{1}{m} \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}\quad (j=1,2,3,...,n)\\ \}\) -
正规方程
\(\theta = (X^TX+\lambda \begin{bmatrix} 0 \; 0 \; 0 \; ... \; 0 \\ 0 \; 1 \; 0 \; ... \; 0 \\ 0 \; 0 \; 1 \; ... \; 0 \\ ...\\ 0 \; 0 \; 0 \; ... \; 1 \end{bmatrix} )^{-1}X^Ty\)
\(\lambda\) 后跟的是(n+1)*(n+1)的矩阵
可以证明,当\(\lambda\)>0时,括号内的矩阵始终可逆。
正则化逻辑回归
- 梯度下降与线性回归相同
- 高级优化

课程链接:
The problem of Overfitting
Cost Function
Regularized Linear Regression
Regularized Logistic Regression