逻辑回归模型(Logistic Regression Model)
损失函数(Cost function)
- 前提:
-
数据集: \(\{ (x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}) ,..., (x^{(3)},y^{(3)}) \}\)
- m个样本 \(x \in \begin{bmatrix} x_0 \\ x_1 \\ ... \\ x_n \end{bmatrix} \quad x_0=1,y \in \{0,1\}\)
- 假设函数 \(h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}\)
-
-
回顾线性回归模型的损失函数:
\(J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \frac{1}{2} {(h_\theta(x^{(i)})-y^{(i)})}^2\)
令:
\(Cost(h_\theta(x^{(i)}), y^{(i)}) = \frac{1}{2}{(h_\theta(x^{(i)}) - y^{(i)})}^2\)
简化为:
\(Cost(h_\theta(x), y) = \frac{1}{2}{(h_\theta(x) - y)}^2\)
将其应用于逻辑回归模型,logistic function 作为假设函数时,其损失函数是非凹的(non-convex):
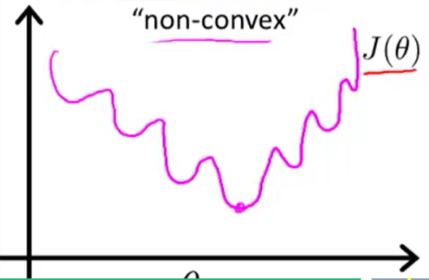
故当基于此运行梯度下降时, 将无法保证收敛于全局最小值 - 逻辑回归损失函数的Cost部分
\(Cost(h_\theta(x),y)= \begin{cases}-\log (h_\theta(x)) \quad if \; y=1 \\- \log (1-h_\theta(x)) \quad if \; y=0 \end{cases}\)
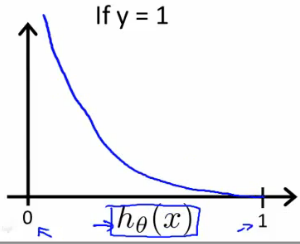
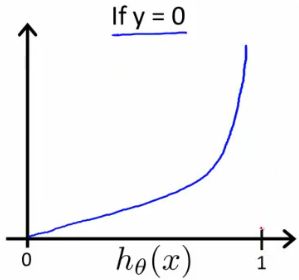
可以看出,在y=1的情况下:若 \(h_\theta(x)=1\) ,则Cost=0;但是当 \(h_\theta(x) \to 0\) 时,\(Cost \to \infty\) 。 y=0时同理。
简化的损失函数和梯度下降
- 简化后的Cost:
\(Cost(h_\theta(x), y)=-y\log(h_\theta(x)) - (1-y)log(1-h_\theta(x))\) - 最终的逻辑回归损失函数:
\(\begin{align*} J(\theta) &= \frac{1}{m} \sum_{i=1}^m Cost(h_\theta(x^{(i)}),y^{(i)}) \\ &= -\frac{1}{m}[\sum_{i=1}^m y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)}))] \end{align*}\)
它用到了最大似然估计 - 向量化的实现: \(h=g(X\theta) \\ J(\theta)=\frac{1}{m} (-y^T\log(h) - (1-y)^T\log(1-h))\)
- 梯度下降与线性回归方法相同:
\(\begin{align*} &Repeat\{\\ &\theta_j := \theta_j-\alpha \frac{\partial}{\partial \theta_j}J(\theta)\\ &\} \end{align*}\)
求偏导得:
\(\begin{align*} &Repeat\{\\ &\theta_j := \theta_j-\alpha \frac{\partial}{m} {\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}}\\ &\} \end{align*}\)
向量化的实现:
\(\theta := \theta - \frac{\alpha}{m}X^T (g(X\theta)-\overrightarrow{y})\)
高级优化
- 对于给定的\(\theta\),我们需要代码来计算以下两个式子:
\(J(\theta)\) \(\frac{\partial}{\partial \theta_j}J(\theta)\) - 优化算法:
- 梯度下降(Gradient descent)
- 共轭梯度(Conjugate gradient)
- BFGS
- L-BFGS
- 另三种算法的优势:
- 不需要手动选择步长α
- 通常比梯度下降要快
- 另三种算法的劣势:
- 复杂
- 不建议自己手写而是最好通过调用库来使用这些算法。库中的算法已经被高度优化。在octave中,我们可以通过无约束最小化函数fminunc(function minimum uncontraint)来调用高级的优化函数来寻找最小值。
- fminunc是一个优化求解器(optimization solver),用来寻找非约束函数的最小值。有了它你不必再想写梯度下降那样去写循环和设置学习速率。你只需提供损失函数 。
- 优化中的约束通常指的是参数上的约束。例如,约束可能限制参数\(\theta <= 0\)。逻辑回归由于theta可以取任意值故不存在约束。
- 首先我们要给出costFunction:
function [jVal, gradient] = costFunction(theta) jVal = [...code to compute J(theta)...]; gradient = [...code to compute derivative of J(theta)...]; end - 然后设置参数和选项,调用fminunc():
>> options = optimset('GradObj','on','MaxIter','100'); >> initialTheta = zeros(2,1) % 最少两个参数 >> [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options)我们设置
GradObj为on来告诉fminunc我们的costFunction返回损失和梯度。它允许fminunc在为函数找最小值的过程中使用梯度。
此外,我们设置MaxIter为400,即最大迭代次数为400.
- fmincg是另一个优化求解器,使用共轭梯度算法来最小化函数。它的使用与fminunc类似,但是在处理含有大量参数的模型时会更加有效率。
公式推导
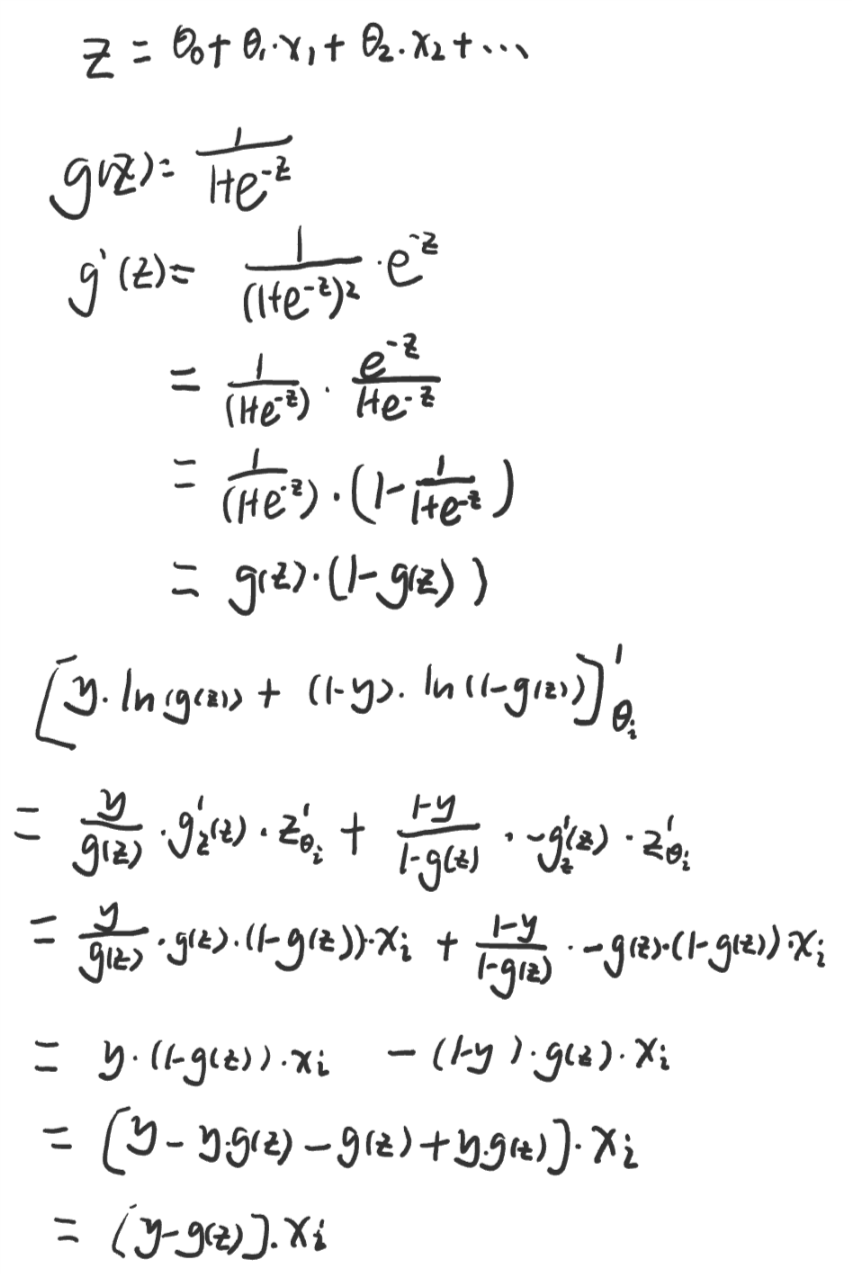
课程链接: