分类及其表示
分类问题(Classification Problem)
当标签y是离散的时候,是为分类问题
例子(二分类问题为例)
- 邮件:垃圾邮件/非垃圾邮件
- 网上交易:虚假的(是/否)
- 肿瘤:恶性的/良性的
\(y \in \lbrace 0, 1 \rbrace \quad\) \(\scriptsize{ 0: “正类” (例如,良性肿瘤)}\\ \scriptsize{ 1:“负类” (例如,恶性肿瘤) }\)
逻辑回归模型(logistic regression model)
- 我们可以忽略y是离散值的事实来处理分类问题,并且使用我们之前的线性回归算法来来尝试对给定的x预测y。然而,我们很容易就可以构造出例子使得该方法执行的结果很差。从直觉上来说,\(h_\theta(x)\) 在超出0到1的范围时同样也是没有意义的。为了解决这个问题,我们可以改变假设的形式来适应y的取值范围。即将 \(\theta^Tx\) 嵌入到 Logistic Function 中。
逻辑回归与线性回归的假设函数具有不同的意义 - 输出值在0到1之间(概率不可能小于0或大于1) \(0 \leq h_{\theta} (x) \leq 1\)
- linear regression function
\(h_\theta(x) = \theta^Tx\) - Logistic function / Sigmoid function
\(h_\theta(x) = g(\theta^Tx) \\ z = \theta^Tx \\ g(z) = \frac{1}{1+e^{-z}}\) 注意 \(\theta^Tx\) 是实数 - 图示:
.png)
- 对假设输出结果的解释 \(h_\theta(x)\) 为:输入x时,y=1的估计的概率
- 例:如果
\(x = \begin{bmatrix}
x_0\\
x_1
\end{bmatrix}
= \begin{bmatrix}
1\\
tumorSize
\end{bmatrix}\)
\(h_\theta(x)=0.7\)
这意味着病人有70%的概率得的是恶性肿瘤。 - 数学表示:
\(h_\theta(x) = P(y=1|x;\theta)\) 且 \(P(y=0|x;\theta ) + P(y=1|x;\theta) = 1\)
- 例:如果
\(x = \begin{bmatrix}
x_0\\
x_1
\end{bmatrix}
= \begin{bmatrix}
1\\
tumorSize
\end{bmatrix}\)
\(h_\theta(x)=0.7\)
决策边界(Decision Boundary)
- 设当 \(h_\theta(x) \geq 0.5\) 时,预测“y=1”
当 \(h_\theta(x) \lt 0.5\) 时,预测“y=0” - 令 \(h_\theta(x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2)\) ,当 \(-3 + x_1 + x_2 \ge 0\) 时,预测“y=1”。则图中红色的直线即为决策边界。
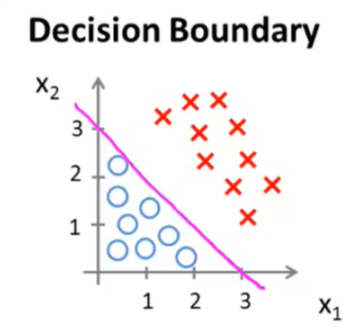
- 决策边界不是训练集的属性,而是假设本身及其参数的属性。
- 我们不是用训练集来定义决策边界,而是用训练集来拟合参数 \(\theta\)
课程链接: