核密度估计 (KDE)
参数估计与非参数估计
参数估计需要预设分布,非参数估计不预设分布。
介绍
概述: 在统计学中,核密度估计(KDE, Kernel Density Estimation)是一个用来估计一个随机变量的概率密度函数的非参数的方法。
输入是样本,输出是概率密度函数。
为方便我们假设数据是一维的。样本独立同分布,有 N 个,如 (-2.1, -1.3, -0.4, 1.9, 5.1, 6.2, …)。
用直方图估计概率密度
显然, 样本越密集的地方, 概率密度越高。对于这种特性,我们很容易联想到直方图:样本越密集的 bin 越高。我们估计概率密度,一个很朴素的思想是,以x轴为样本的值,以y轴为概率密度,构建起一个直方图。令每个样本贡献 1/N 的概率密度,若一个bin里有6个样本,那么它的高度就为 6/N。这样,就得到了一个分段的概率密度函数,同一个bin中的样本具有相同的概率密度。直观上来说,概率密度函数就是取直方图每个bin的顶部的那段横线,所得到的分段函数。
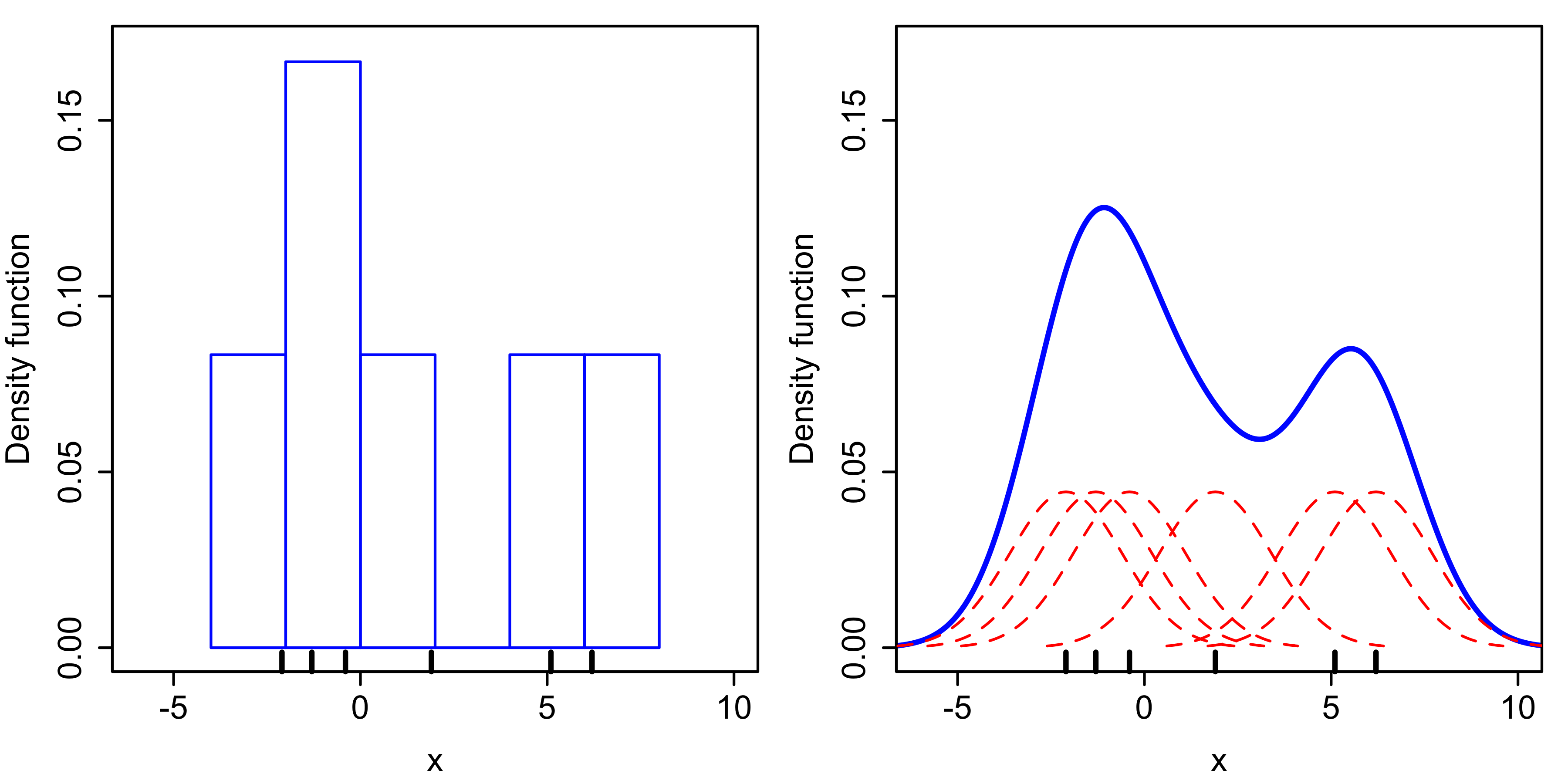
但是,同一个bin中的样本具有相同的概率密度显然不合理。我们希望有一个平滑可导的概率密度函数。
为了实现这个目的,首先可以考虑,无限减小bin的宽度,每个样本只在其对应的x坐标处贡献 1/N 的概率密度。但这会产生另一个问题: 样本中没有出现的值,概率为0,概率密度函数不连续。
\[f(x)=sampleNumberAt(x)\frac{1}{N}\]卷积平滑与 Kernel
于是,我们考虑,利用邻域的信息来对概率密度函数做平滑。核密度估计的本质:卷积平滑(图2)。图像处理中的图像的去噪平滑也是同样的原理。
平滑需要选择kernel function, 这个东西在机器学习图像处理中都很常见,就不细讲了。总之,不同的kernel产生不同的效果。下图列出了常见kernel的形状。一般采用标准正态分布对应的高斯核(normal)。
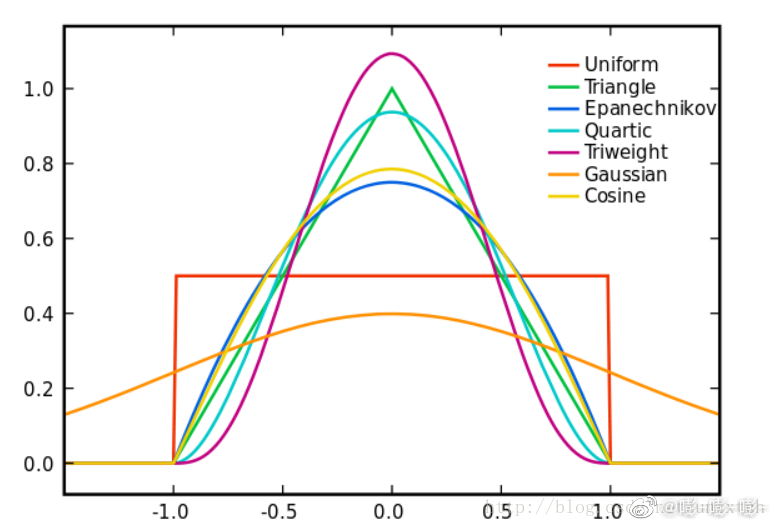
公式
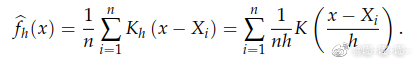

bandwidth
公式中的h会影响卷积核的宽度。h越大,影响到某点概率密度的样本就越多,概率密度函数就越平滑。由于只是在做平滑,显然最后得到的概率密度函数的形状,大致和bin宽度为2h的直方图的形状还是一样的。
h的选择,显然可以用交叉验证法。也有很多其他的选择算法。
可视化中的应用
KDE 在可视化中有很多应用。
- 点线图:edge-bundling,突出网络的趋势。
- 折线图:对折线做平滑,突出折线的趋势。
- 密度图:对于线密度图有升级版的 CDE (Curve Density Estimation),CDE 有考虑到折线的连续性。
参考资料: