Blog

懒癌晚期

Project maintained by VirusPC Hosted on GitHub Pages — Theme by mattgraham

Back Home

正则化

引出

给定数据集 \(D=\{(x_1,y_1),\ (x_2,y_2),\ ...,\ (x_m,y_m) \}\) ，其中 \(x \in \mathbb{R}^d\) ， \(y \in \mathbb{R}\) ，我们考虑最简单的线性回归模型，以平方误差为损失函数，则优化目标为：

\[{ \min_{w} \sum_{i=1}^m (y_i-w^Tx_i)^2 }\]

当特征很多而数据集不够大时，该模型会陷入过拟合。为了缓解过拟合问题，我们引入了正则化项（regularization item）。将目标函数与正则化项相加是为正则化。

范数

正则化有两种方式，一种是L1正则化，一种是L2正则化。其中，前者是利用了L1范数，后者是利用了L2范数。
在这里我们先简单的介绍一下L1范数。设存在一个向量 v=[1, -1, 2]，那么该向量的L1范数即为其各元素的绝对值之和，即：
\(||v||_1 = |1|+|-1|+|2| = 4\)
该向量的L2范数即为各元素的平方和开根，即：
\(||v||_2 = \sqrt{(1)^2+(-1)^2+(2)^2}= \sqrt{6}\)

L1正则化

使用L1范数正则化后的目标函数如下：

\[\min_w \sum_{i=1}^m(y_i-w^Tx_i)^2 + \lambda||w||_1\]

其中 \(\lambda \gt 0\) 被称为正则化参数，而上式被称为LASSO（Least Absolute Shrinkage and Selection Operator）回归。

L2正则化

由于加上L2正则化后，权重在更新时会多减去一部分，故L2正则化有时也被称为权重衰减（weights decay）。使用L2范数正则化后的目标函数如下：

\[\min_w \sum_{i=1}^m(y_i-w^Tx_i)^2 + \lambda{||w||_2}^2\]

同样的其正则化参数 \(\lambda >0\) 。上式被称为“岭回归”（ridge regression）

另外，在神经网络中，将L2范数扩展应用到矩阵上，我们通过弗罗贝尼乌斯范数（Frobenius norm）来实现正则化。

\[||w^{[l]}||^2_F = \sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{[l]} (w_{ij}^{[l]})^2\]

L1正则化与L2正则化比较

L1范数和L2范数正则化都有助于降低过拟合风险，让我们通过图像来直观感受一下正则化所带来的改变。假设有两个特征值，同颜色曲线上的点的损失相同。

原函数曲线等值线：
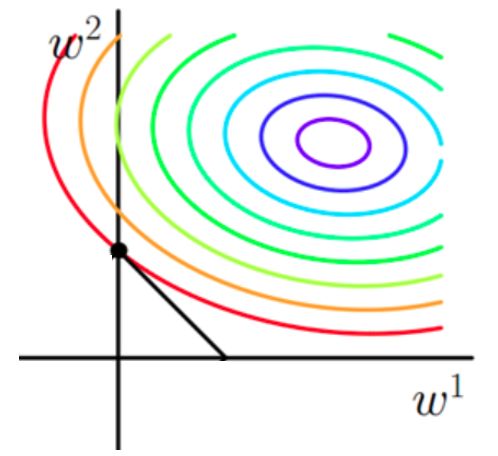
目标函数等高线

分别将L1正则化项和L2正则化项的等值线加入上图后的函数图像：
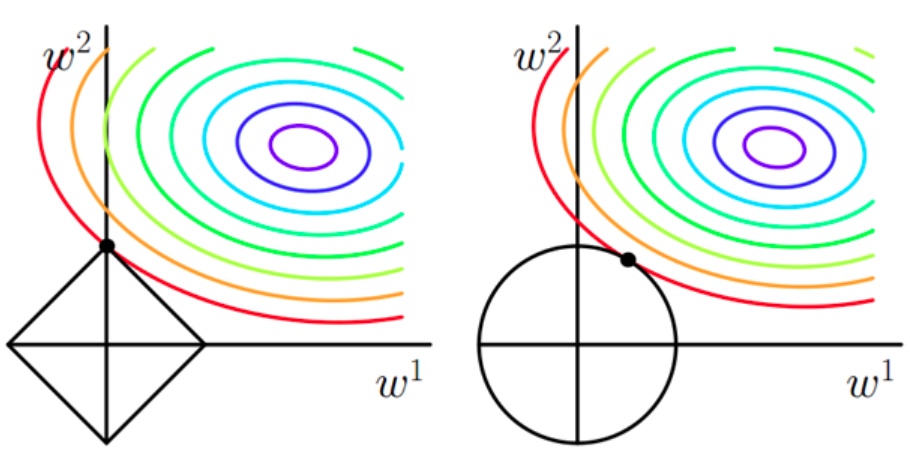
加入L1和L2正则的等高线

在没有正则化项时，对于这种损失函数为凸函数的模型来说，我们要求的最佳的参数值位于最里层的也就是紫色等值线上。
而引入正则化项后，我们不仅要求这个五颜六色的圈要小，还要使正则化项所代表的图像越小越好。注意，平方误差项与正则化项的参数应该是相同的，即我们要选的是二者等值线相交的点。由于二者都是圈越向中心缩小越好，这样一来参数就被正则化项从平方误差等值线的中心拉向坐标轴原点，减小了w1和w2的取值。使得假设函数变得更加平滑而不是猛烈的忽上忽下的剧烈变化，降低了过拟合的风险。
至于正则化参数，我们以L1正则化项为例 假设某条等值线的值为c，即： \(\lambda ||w||_1=c\) ，当我们将正则化参数增大一倍时，在c不变的情况下， \(||w||_1\) 会缩小一倍，可以想象平方误差等值线就会被进一步拉向远点。故增大正则化系数会对目标函数产生更大的影响，更不易发生过拟合。
此外，我们发现： 采用L1范数时交点常出现在坐标轴上，即w1或w2为0；采用L2范数时焦点常出现在某个象限中，即w1和w2均非0。也就说L1正则化是更容易得到稀疏解，L2正则化得到的解更加平滑。
由于w取得稀疏解意味着初始的所有特征中，只有w值不为0的特征值才是我们需要的，才会出现在最终的模型中，这意味着我们可以通过L1正则化来去掉不那么需要的特征值，降低模型的复杂度，其更符合奥卡姆剃刀理论。

L1正则化+L2正则化

当我们同时使用L1范数和L2范数时，就变成了ElasticNet回归，我们可以通过调节 \(\lambda_1\) 和 \(\lambda_2\) 来在稀疏和光滑之间进行平衡：

\[\min_w \sum_{i=1}^m(y_i-w^Tx_i)^2 + \lambda_1 ||w||_1 + \lambda_2{||w||_2}^2\]

随机失活正则化（神经网络中）

更准确的来说，随机失活应该被看作一种自适应形式而不是正则化。使用随机失活技术，我们要设置一个概率值p，然后遍历网络的每一个节点，使他们有p的概率被保留，（1-p）的概率被丢弃。经过随机失活后我们将会得到一个被简化了很多的网络，然后再对其进行训练。这个技术虽然看起来十分疯狂，但它的确是有效的。

实现随机失活算法的方法有很多，这里我们讲一下最常用的一种：反向随机失活（inverted dropout)。它主要分为4步：

  1. 为第l层的权重矩阵生成一个与其形状一致的，元素值为0~1的随机矩阵\(a_l\)。
  2. 设置keep_prob，值在0~1之间，表示该层节点保留的概率。（每层可以不同，与输出层关联的层为1，输入层一般为1，但在图像识别中输入往往是全部像素值，比较大，一般不设为1）
  3. 将\(a_l\)中的每个元素与keep_prob相比较，将比较结果保存到新的矩阵\(d_l\)中。若小于keep_prob则将\(d_l\)同位置的元素置为1，表示保留；大于则将\(d_l\)同位置的元素置为0，表示删除。
  4. 将\(a_l\)与\(d_l\)点乘，得到新的权重矩阵\(a_l\)
  5. \(a_l\)中的每个元素都除以keep_prob。此步是为了保证\(a_{l}\)的期望值不变。

注意，如果用同一个训练集进行迭代，在不同的训练轮次中，你应该随机地将不同的隐藏单元清零，而不是每次迭代都丢弃同一组隐藏单元。此外，我们不应该在测试阶段使用随机失活算法。我们不希望测试结果也是随机的。

随机失活技术的成功应用大多实在计算机视觉领域中。因为在这个领域中，他的输入层要包含每个像素点的值，而特征值越多需要的数据集就越多，几乎不可能有足够的数据。在计算机视觉领域中使用它几乎已经成为一种默认了。但需要记住随机失活是一种正则化技术，目的是防止过拟合，只有在发生过拟合时才应该去考虑他。

随机失活的另一个缺点是让代价函数变得不那么明确。因为每一次迭代都有一些神经元随机失活。所以当你取检验梯度下降算法的表现的时候，你会发现很难确定代价函数是否已经定义的足够好（随着迭代值不断变小），因此也难以通过绘制学习曲线来确保代码正常运行。

早停（early stopping）

通过绘制学习曲线找到测试误差最小的时候对应的迭代次数，提前停止迭代。

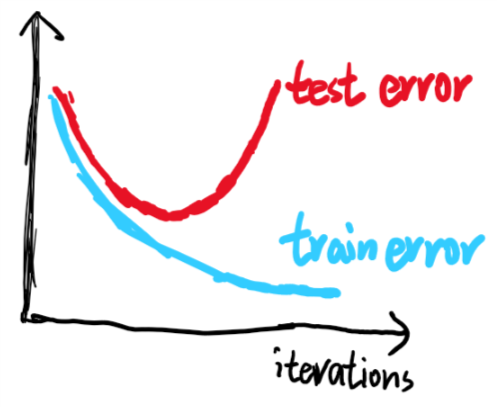
learning curve

我们一般把机器学习过程看作是几个步骤的组合，每一步只专注于做自己的事，其中之一是利用优化函数来优化代价函数。当你专注于优化成本函数时，你在乎的只是找到合适的权重，使得损失J尽可能地小。然而避免过拟合是另外一项完全不同的任务，在做这件事时你有一套完全不同的工具来解决这个问题。在同一时间只考虑一个任务的原则又被称为正交化（orthogonalization）。而早停的主要缺点就是把两个任务结合了，因为提早停止了梯度下降意味着打断了优化代价函数的过程，这样在优化代价函数这项任务上就会做的不够好。用一个工具解决两个问题会变得更复杂。我们可以选择L2正则化来代替早停，那么你就可以专注于优化代价函数，尽可能久的训练神经网络。使用L2正则化的缺点是你可能需要尝试大量的正则化参数lambda的值才能找到合适的，计算代价比较高。二者各有利弊。

课程链接：

参考资料：