偏差(Bias)与方差(Variance)
当你运行一个学习算法时，如果这个算法的表现不理想，那么多半时出现两种情况：要么是偏差比较大，要么是方差比较大。换句话说，出现的情况要么是欠拟合，要么是过拟合。这两种情况哪个和偏差有关，哪个和方差有关，或者是不是和两个都有关，搞清楚这点非常重要。判断出是那种情况对我们改进算法很有帮助。
概念
泛化误差=偏差+方差+噪声
- 偏差度量了学习算法的期望预测与真实结果的偏离程度，刻画了学习算法本身的拟合能力。高偏差时，期望预测与真实结果偏差巨大，出现欠拟合。
- 方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。高方差时，训练集轻微的变化都会导致学习算法的剧烈变化，出现过拟合。
- 噪声表达了在当前任务生任何学习算法所能达到的期望泛化误差的下界（此时偏差和方差都为0），即刻画了学习问题本身的难度。
一般来说，偏差与方差是有冲突的，这成为偏差-方差窘境（bias-variance dilemma）。给定学习任务，假定我们能控制学习算法的训练程度，则在训练不足时，学习器的拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导了泛化错误率； 随着训练程度的加深，学习器的拟合能力逐渐增强，训练数据发生的扰动渐渐能被学习器学到，方差逐渐主导了泛化错误率； 在训练程度充足后，学习器的拟合能力已非常强，训练数据发生的轻微扰动都会导致学习器发生显著变化，若训练数据自身的、非全局的特性被学习器学到了，则发生过拟合。
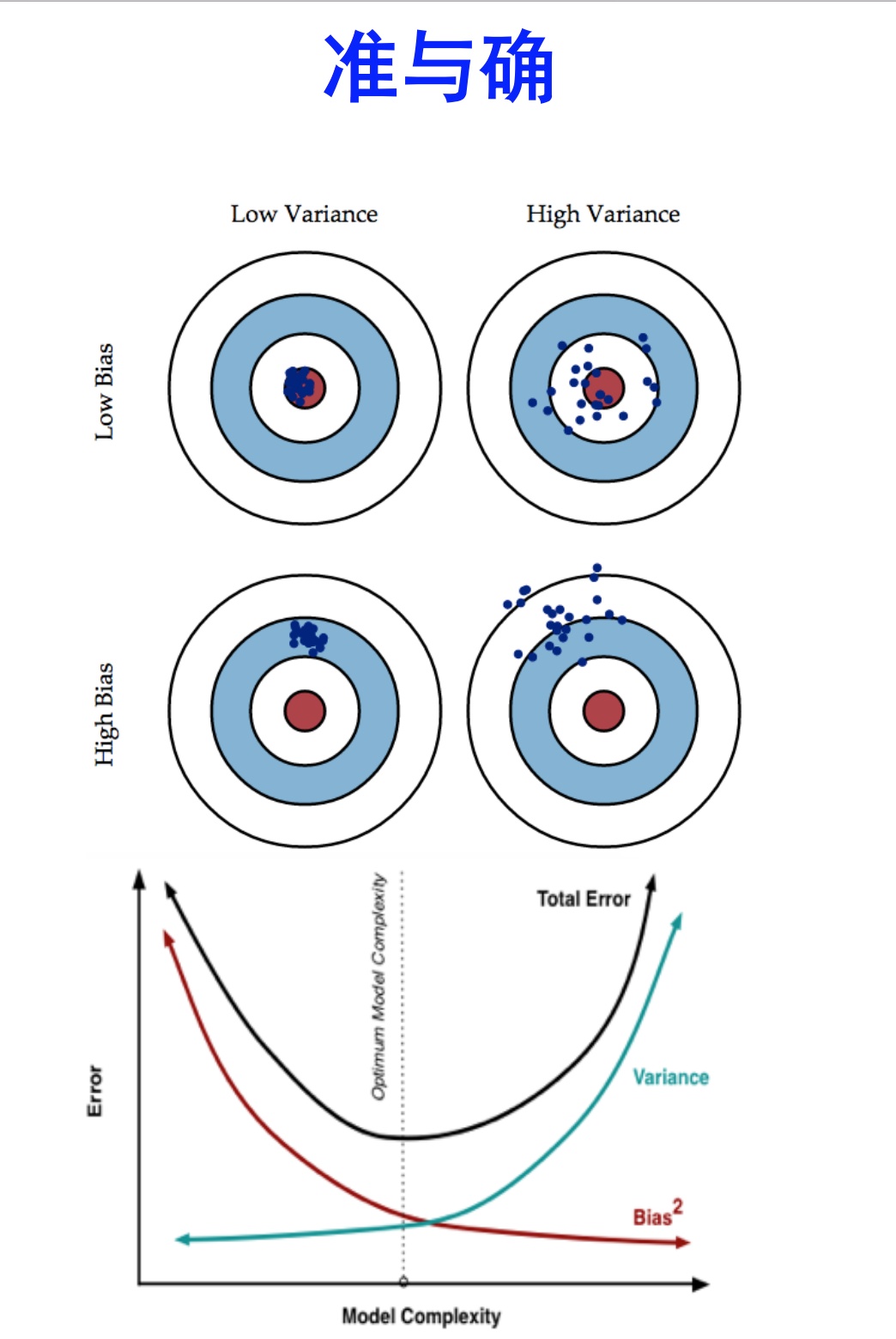
假设红色的靶心区域是学习算法完美的正确预测值, 蓝色点为每个数据集所训练出的模型对样本的预测值, 当我们从靶心逐渐向外移动时, 预测效果逐渐变差.
特征多项式维度与偏差/方差
训练集与交叉验证集 的 特征多项式维度与损失的关系：
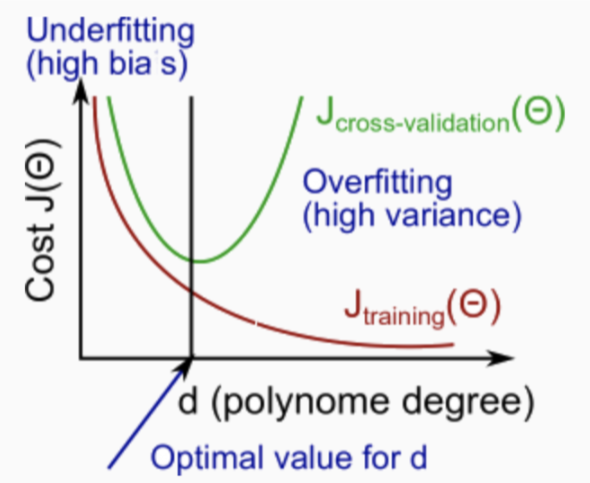图中偏左,即 \(J_{train}(\theta)\) 很高且 \(J_{cv}(\theta) \approx J_{train}(\theta)\) 时，会产生高偏差（欠拟合）问题；
偏右，即 \(J_{train}(\theta)\) 很低且 \(J_{cv}(\theta) \gg J_{train}(\theta)\) 时，会产生高方差（过拟合）问题。
正则化与偏差/方差
正则化只是在优化过程中使用，在计算 \(J_{train}(\theta)\)、\(J_{cv}(\theta)\) 和 \(J_{test}(\theta)\) 时并不会用到。
当较小时，我们的假设函数会倾向于欠拟合；当lambda较大时，我们的假设函数会倾向于欠拟合。为了选择模型和正则项lambda，我们需要：
- 创建一个lambda的列表，例如：{0, 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.64, 1.28, 2.56, 5.12, 10.24}
- 创建一个不同维度或任何其它不同变量的模型
- 遍历lambda列表，对每个lambda，检查所有的模型来学习参数。
- 使用习得的参数计算交叉验证误差\(J_{cv}(\theta)\)，注意\(J_{cv}(\theta)\)不包括正则化项或令lambda为0。
- 使用交叉验证误差最小的的参数和lambda，计算\(J_{test}(\theta)\),观察其是否具有良好的泛化能力。
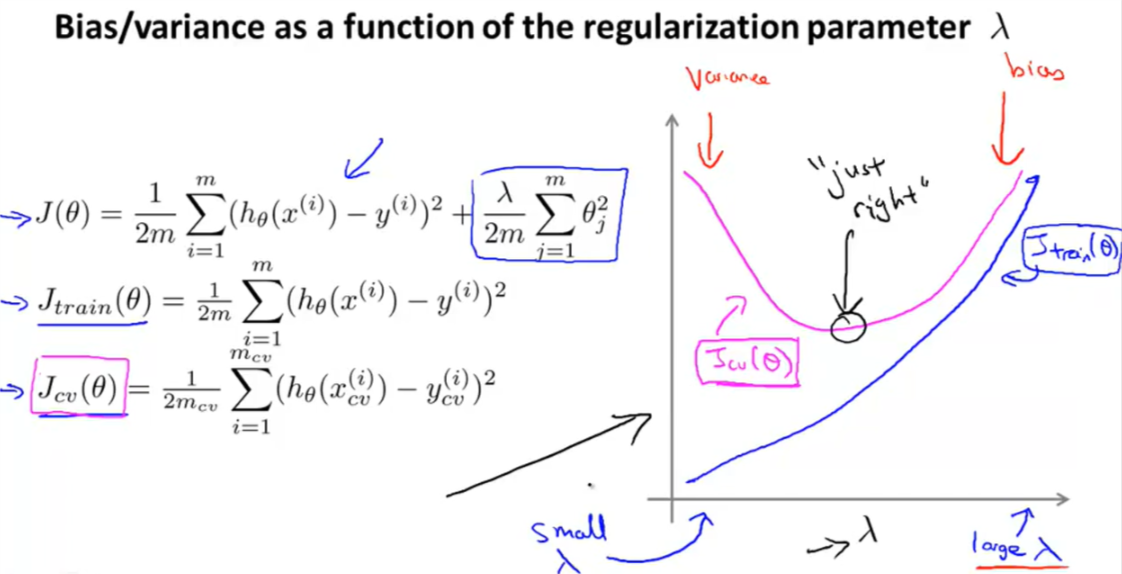
lambda与损失的关系:
学习曲线
使用很少的样本来训练模型，由于很容易找得到完全经过这些点的曲线，所以很容易得到0误差。由此：
- 我们的训练集越大，函数的误差越大
- 误差在m到达某个值或者说训练集达到某个规模后之后会达到平衡
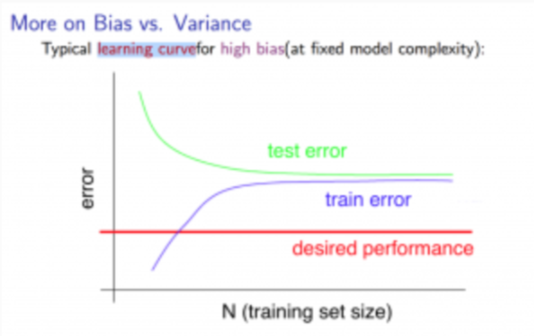
在模型具有高偏差的情况下(由于特征过少而导致的高偏差)：
- 小的训练集：导致 \(J_{train}(\Theta)\) 低，\(J_{cv}(\Theta)\) 高。
- 大的训练集：导致 \(J_{train}(\Theta)\) 和 \(J_{cv}(\Theta)\)都高，且 \(J_{train}(\Theta) \approx J_{cv}(\Theta)\) 。
如果一个学习算法具有高偏差，获取更多的训练数据可能不会提供显著的帮助。
在模型具有高方差的情况下（由于特征过多而导致的高方差）：
- 小的训练集：\(J_{train}(\Theta)\) 趋向于低，\(J_{cv}(\Theta)\) 趋向于高。
- 大的训练集：\(J_{train}(\Theta)\) 随着训练集规模的增加而增加，并且 \(J_{cv}(\Theta)\) 未达到平衡而是持续下降。同样的，\(J_{train}(\Theta) < J_{cv}(\Theta)\)，但是他们之间的差距显著。
如果一个学习算法具有高方差，由于两个曲线理应趋向于同一水平线，故额外增加训练数据会有帮助。
如何提升算法性能
回顾之前我们的选项：
- 获取更多的样本 —— 解决高方差
- 尝试更小的特征集 —— 解决高方差
- 尝试获取额外的特征 —— 解决高偏差
- 尝试添加多项式特征 —— 解决高偏差
- 尝试减小lambda —— 解决高偏差
- 尝试增加lambda ——解决高方差
神经网络
- 输入层单元个数
如果一个神经网络具有较少的参数，就会倾向于欠拟合，计算开销小。
一个有很多参数的大神经网络会倾向于过拟合，计算开销大。因此你可以使用正则化来解决它，这要比减小神经网络规模更好。 - 隐含层层数
使用一个隐含层是一个好的默认的开始。你也可以使用交叉验证集来训练具有多层隐含层的神经网络，然后选择性能最好的一个。 - 各个隐含层的单元个数 为隐含层设置过多的单元也会导致过拟合。
课程链接：
- Diagnosing Bias vs. Variance
- Regularization and Bias/Variance
- Learning Curves
- Deciding What to Do Next Revisited
其它参考资料：
- [1]周志华.机器学习[M].北京:清华大学出版社,2016：44-46.